We have observed strong correlations between the r-process and s-process
elements abundances and the  elements abundances in field metal-poor
stars. We explain those correlations with the EASE scenario, which closely
links the origin of these stars to globular clusters.
According to this scenario, thick disk and field halo stars were born in
globular clusters from which they escaped, either during an early
disruption of the cluster (forming Pop IIa) or through a later disruption
or an evaporation process (Pop IIb). We assume that before escaping from
the globular cluster the PopIIb stars will accrete some of the s-process
elements matter which is ejected by the intermediate-mass stars when they
reach the Asymptotic Giant Branch.
Here we examine and compare three different accretion situations.
If the globular cluster's binding potential is strong enough, the gas
ejected by the AGB stars can sink to the cluster's center and form a
reservoir from which the lower-mass stars can accrete matter.
If the binding potential is not strong enough, the gas will flow out of
the cluster, and the stars can accrete from this flow. And, finally,
main sequence stars in the cluster can accrete gas during close encounters
with mass-losing AGB stars.
elements abundances in field metal-poor
stars. We explain those correlations with the EASE scenario, which closely
links the origin of these stars to globular clusters.
According to this scenario, thick disk and field halo stars were born in
globular clusters from which they escaped, either during an early
disruption of the cluster (forming Pop IIa) or through a later disruption
or an evaporation process (Pop IIb). We assume that before escaping from
the globular cluster the PopIIb stars will accrete some of the s-process
elements matter which is ejected by the intermediate-mass stars when they
reach the Asymptotic Giant Branch.
Here we examine and compare three different accretion situations.
If the globular cluster's binding potential is strong enough, the gas
ejected by the AGB stars can sink to the cluster's center and form a
reservoir from which the lower-mass stars can accrete matter.
If the binding potential is not strong enough, the gas will flow out of
the cluster, and the stars can accrete from this flow. And, finally,
main sequence stars in the cluster can accrete gas during close encounters
with mass-losing AGB stars.
1. Introduction

|
We have obtained accurate relative abundances for a sample of 21 mildly
metal-poor field stars from the analysis of high resolution, high
signal-to-noise spectra (Jehin et al. 1999a).
Looking for correlations between the element abundances, we found that the
 -elements and the iron-peak elements are
well correlated with each
other, and the abundances of the rapid neutron-capture elements
(r-process elements) are well correlated with those of the
-elements and the iron-peak elements are
well correlated with each
other, and the abundances of the rapid neutron-capture elements
(r-process elements) are well correlated with those of the
 -elements, which is in
agreement with the generally accepted idea that those elements are produced
during the explosion of massive stars. For the slow neutron-capture
elements (s-process elements),
we find that the stars can be separated into two subpopulations. For those
in PopIIa, the abundances of the s-process elements vary little
while that of the
-elements, which is in
agreement with the generally accepted idea that those elements are produced
during the explosion of massive stars. For the slow neutron-capture
elements (s-process elements),
we find that the stars can be separated into two subpopulations. For those
in PopIIa, the abundances of the s-process elements vary little
while that of the  elements increases up
to a maximum value. The stars in PopIIb show a large range in their
s-process elements abundances, while
they show a constant and maximum value for the abundances of the
elements increases up
to a maximum value. The stars in PopIIb show a large range in their
s-process elements abundances, while
they show a constant and maximum value for the abundances of the
 elements. We called this behavior the "two-branches diagram".
To explain this result, we have
developed the EASE scenario, which links the metal-poor
field stars to the globular clusters. The observations and the EASE
scenario are described in more details in Jehin et al. (1999a, 1999b).
elements. We called this behavior the "two-branches diagram".
To explain this result, we have
developed the EASE scenario, which links the metal-poor
field stars to the globular clusters. The observations and the EASE
scenario are described in more details in Jehin et al. (1999a, 1999b).
One crucial piece of this scenario consists in explaining how unevolved
stars (PopIIb) can get enriched in s-process elements while the
 elements abundances remain
constant. The s-process elements are mainly produced in asymptotic giant
branch (AGB) stars, where they are brought to the surface through dredge-up
processes.
The AGB stars lose a large fraction of their mass through stellar winds or
superwind events, releasing the s-process elements enriched gas in the
interstellar medium. Main sequence stars can accrete this matter, thereby
enriching their surface abundances in those elements.
elements abundances remain
constant. The s-process elements are mainly produced in asymptotic giant
branch (AGB) stars, where they are brought to the surface through dredge-up
processes.
The AGB stars lose a large fraction of their mass through stellar winds or
superwind events, releasing the s-process elements enriched gas in the
interstellar medium. Main sequence stars can accrete this matter, thereby
enriching their surface abundances in those elements.
The idea that the gas ejected by the AGB stars in globular clusters can be
accreted by other stars in the cluster is not an entirely new one.
Observations of globular clusters show that they contain much too little gas
or dust, compared to what is lost by their AGB stars, and globular cluster
stars also show many abundance anomalies.
Many authors have been intrigued by the fate of the gas in globular clusters,
and among them, Scott & Rose (1975),
Faulkner & Freeman (1977), VandenBerg & Faulkner (1977), VandenBerg (1978),
and Scott & Durisen (1978), and accretion has already been suggested as a
plausible mechanism to explain abundance anomalies
(D'Antona et al. 1983, Faulkner 1984, Faulkner & Coleman 1984,
Smith 1996).
In order for accretion
to be efficient, the gas density should be as high as possible, the relative
velocity of the accreting star with respect to the gas should be low, and the
time during which the accretion takes place should be long.
5. Conclusions

|
We have investigated different gas accretion processes in globular clusters,
namely, accretion from a central reservoir of gas, accretion from a cluster
wind,
and accretion during close encounters with mass-losing stars. By far the
most promising process is the first one.
We argue that accretion of gas by globular cluster stars has to take place,
at least to some degree, and that it could be large in some cases. Furthermore,
even a small amount of accretion will affect the surface composition of
main sequence stars. The amount of accretion will depend on many
parameters, such as the stellar initial mass, velocity, and orbit in the
cluster, the cluster's core radius, concentration, mass, and orbit in the
Galaxy, the AGB ejecta speed, etc... so that the accretion will be highly
variable from star to star.
References

|
Bahcall, J.N., Piran, T., 1983, ApJ 267, L77
Bondi, H., 1952, MNRAS 112, 195
D'Antona, F., Gratton, R.G., and Chieffi, A., 1983, MSAIt 54, 173
Faulkner, D.J. and Freeman, K.C., 1977, ApJ 211, 77
Faulkner, D.J., 1984, MNRAS 206, 109
Faulkner, D.J., and Coleman, C.S., 1984, MNRAS 206, 121
Jehin, E., Magain, P., Neuforge, C., Noels, A., Parmentier, G.,
Thoul, A.A., 1999a, A&A 341, 241
Jehin, E., Magain, P., Neuforge, C., Noels, A., Parmentier, G.,
Thoul, A.A., 1999b, in Proceedings of the 35th Liège International
Astrophysical Colloquium: "The Galactic Halo: From Globular Clusters
to Field Stars", ed. A. Noels, P. Magain, D. Caro, E. Jehin,
G. Parmentier, and A. Thoul.
Scott, E.H. and Rose, W.K., 1975, ApJ 197, 147
Scott, E.H., and Durisen, R.H., 1978, ApJ 222, 612
Smith, G.H., 1996, PASP 108, 176
VandenBerg, D.A., and Faulkner, D.J., 1977, ApJ 218, 415
VandenBerg, D.A., 1978, ApJ 224, 394
Weidemann, V., and Koester, D., 1983, AA 121, 77
Retour
Back
Institut d'Astrophysique et de
Géophysique de l'
Université de Liège
Avenue de Cointe, 5
B-4000 Liège, BELGIQUE
Tel: +32 (0)4 252.99.80
Fax: +32 (0)4 252.74.74
Web pages:
Sandrine Sohy
Last modification: October,5 2000.
 elements abundances in field metal-poor
stars. We explain those correlations with the EASE scenario, which closely
links the origin of these stars to globular clusters.
According to this scenario, thick disk and field halo stars were born in
globular clusters from which they escaped, either during an early
disruption of the cluster (forming Pop IIa) or through a later disruption
or an evaporation process (Pop IIb). We assume that before escaping from
the globular cluster the PopIIb stars will accrete some of the s-process
elements matter which is ejected by the intermediate-mass stars when they
reach the Asymptotic Giant Branch.
Here we examine and compare three different accretion situations.
If the globular cluster's binding potential is strong enough, the gas
ejected by the AGB stars can sink to the cluster's center and form a
reservoir from which the lower-mass stars can accrete matter.
If the binding potential is not strong enough, the gas will flow out of
the cluster, and the stars can accrete from this flow. And, finally,
main sequence stars in the cluster can accrete gas during close encounters
with mass-losing AGB stars.
elements abundances in field metal-poor
stars. We explain those correlations with the EASE scenario, which closely
links the origin of these stars to globular clusters.
According to this scenario, thick disk and field halo stars were born in
globular clusters from which they escaped, either during an early
disruption of the cluster (forming Pop IIa) or through a later disruption
or an evaporation process (Pop IIb). We assume that before escaping from
the globular cluster the PopIIb stars will accrete some of the s-process
elements matter which is ejected by the intermediate-mass stars when they
reach the Asymptotic Giant Branch.
Here we examine and compare three different accretion situations.
If the globular cluster's binding potential is strong enough, the gas
ejected by the AGB stars can sink to the cluster's center and form a
reservoir from which the lower-mass stars can accrete matter.
If the binding potential is not strong enough, the gas will flow out of
the cluster, and the stars can accrete from this flow. And, finally,
main sequence stars in the cluster can accrete gas during close encounters
with mass-losing AGB stars.

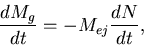
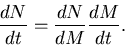
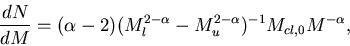
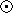 )
to its lifetime on the main sequence t (in
years) (Bahcall & Piran 1983)
)
to its lifetime on the main sequence t (in
years) (Bahcall & Piran 1983)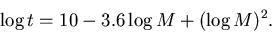
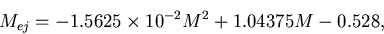
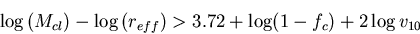
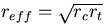 is the cluster's effective radius (in parsec),
rc and rt are the cluster's core and tidal
radii, fc is the fraction of the initial ejecta energy lost via
radiative cooling and v10 is the stellar-ejecta speed
in units of 10 km/s. He also shows that many Galactic globular clusters obey
this relation, using present-day parameters.
Therefore, in tightly bound
globular clusters, the gas released by the AGB stars can be retained in the
cluster's center, forming a central reservoir of gas. The gas will accumulate
in the cluster's center between passages through the galactic plane, at which
time the cluster will be swept clean of the gas.
is the cluster's effective radius (in parsec),
rc and rt are the cluster's core and tidal
radii, fc is the fraction of the initial ejecta energy lost via
radiative cooling and v10 is the stellar-ejecta speed
in units of 10 km/s. He also shows that many Galactic globular clusters obey
this relation, using present-day parameters.
Therefore, in tightly bound
globular clusters, the gas released by the AGB stars can be retained in the
cluster's center, forming a central reservoir of gas. The gas will accumulate
in the cluster's center between passages through the galactic plane, at which
time the cluster will be swept clean of the gas. 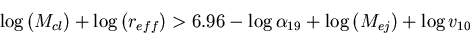
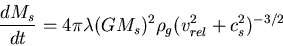
 g is the unperturbed gas
density, vrel is the relative velocity of the star with respect to
the gas, cs is the sound speed in the gas, and
g is the unperturbed gas
density, vrel is the relative velocity of the star with respect to
the gas, cs is the sound speed in the gas, and
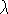 is a parameter of order 1.
is a parameter of order 1.
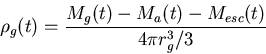
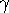 of its lifetime inside the gas reservoir,
as its orbit in the cluster will take it out of the gas reservoir. We
therefore write
of its lifetime inside the gas reservoir,
as its orbit in the cluster will take it out of the gas reservoir. We
therefore write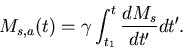
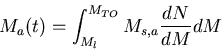
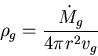
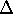 t ~ b/vrel.
We get
t ~ b/vrel.
We get 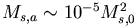 for
for
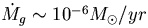 ,
vg ~ 10 km/s,
vrel ~ 10 km/s and b = 1au.
This result should be multiplied by the number of encounters the main
sequence star will have with AGB stars during its lifetime. We expect however
the accretion through this process to be much less efficient than the accretion
from a central reservoir of gas.
,
vg ~ 10 km/s,
vrel ~ 10 km/s and b = 1au.
This result should be multiplied by the number of encounters the main
sequence star will have with AGB stars during its lifetime. We expect however
the accretion through this process to be much less efficient than the accretion
from a central reservoir of gas.