We present a model of globular cluster self-enrichment.
In the protogalaxy, cold and dense clouds embedded in the hot
protogalactic medium are assumed to be the progenitors of galactic halo
globular clusters (GCs). The massive stars of a first generation, born in the
central regions of proto-globular cluster clouds (PGCCs), explode as Type
II supernovae (SNeII). The associated blast waves trigger the expansion of a
supershell enriched by the heavy elements released by these massive
stars. A second generation of stars, born in the shell, will lately
form the GCs.
We revisit the most often encountered argument against
self-enrichment, namely the presumed ability of a small number of
supernovae to disrupt PGCCs. With a model of the dynamics of the
supershell and of its progressive chemical enrichment, it is shown that
the minimal mass required to avoid disruption by several tens of SNeII
is compatible with the masses usually assumed for PGCCs within the
context of the Fall and Rees theory (1985). Furthermore,
the corresponding self-enrichment level is in agreement with the halo
GC metallicities.
1. Introduction

|
The Liege group currently develops a scenario about the chemical evolution of
galactic globular clusters.
This scenario aims to explain two subpopulations
of halo and thick disk field stars by linking them
to two distinct stages in the chemical evolution of GCs, a Type II supernova
(SNII) phase and an accretion phase (Jehin et al., Section II,
Thoul et al., this section).
The scenario is therefore labelled EASE (Evaporation/Accretion/
Self-Enrichment).
The purpose of this work is to investigate the possibility of the
SNII phase from a dynamical point of view (Parmentier et al., 1999).
2. GC Formation Through Supershell
Phenomenon

|
We adopt the Fall and Rees (1985) theory as a description of the protogalaxy.
Namely, dense and cold (T ~ 104K)
clouds embedded in a diffuse and hot
(T ~ 2 × 106K)
protogalactic background are assumed to be the
progenitors of galactic globular clusters.
These PGCCs are assumed to be
isothermal spheres in pressure equilibrium with the hot protogalactic
background confining them. According to the Schmidt law, the denser
the medium is, the quicker the stars will form. We therefore expect that the
first stars that will form in the PGCCs will be centrally
concentrated.
After a few millions years, the massive stars of this first generation
explode as SNeII. The blast waves associated with these explosions
trigger the expansion of a supershell in which all the cloud material
is swept up. Concurrently, the shell of gas is chemically enriched by the
heavy elements released by the exploding massive stars.
This is the self-enrichment process: the primordial cloud has
produced its own source of chemical enrichment.
The question then is whether this self-enrichment process is
able to explain the metallicities currently observed in the
galactic halo GCs.
In these compressed and enriched layers of gas, the formation of a second
generation of stars is triggered. These stars can recollapse and form a GC.
Such a formation scenario was successively proposed and developed by
Cayrel (1986) and Brown, Burkert and Truran (1991, 1995).
Despite these works, a recurrent argument was used
against the possibillity of a self-enrichment phase in GCs.
By comparing the kinetic
energy of the ejecta of just one SNII and the binding energy of
a still gaseous protoglobular cluster, several authors
have concluded that this one could be immediatly
disrupted. Therefore, from this point of view, GCs could not be
self-enriched systems.
However, it is important to point out that there is a difference between
the kinetic energy of a SNII ejecta and the kinetic
energy of the Interstellar Medium (ISM) : not all the
kinetic energy of the ejecta is deposited as kinetic energy of the ISM.
We therefore propose to revisit this argument. We suggest another criterion
for disruption : the comparison between the binding energy of the cloud
and the kinetic energy of the supershell when it emerges from the initial
cloud (when all the cloud has been swept up in the supershell).
6. Self-Enrichment Level

|
The previous dynamical criterion defines a maximum number of SNeII for a
given mass.
As we deal with a process of self-enrichment, we now check whether this
SNII number is able to enrich the primordial gas up to
galactic halo metallicities.
For a given mass of primordial gas and a given Initial Mass Function (IMF),
here a Salpeter one, we compute the number of SNeII necessary to
reach a given final metallicity. All supernovae whose mass m is
between 12 and 60 M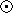 are assumed to
release a mass mz=0.3m-3.5
(in units of M
are assumed to
release a mass mz=0.3m-3.5
(in units of M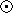 )
of heavy elements. The total number of supernovae also take into
account those whose mass is between 9 and
12 M
)
of heavy elements. The total number of supernovae also take into
account those whose mass is between 9 and
12 M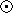 .
Indeed, even if they release negligible amounts of heavy elements,
their dynamical impact on the PGCC must be considered.
From the comparison between these iso-metallicity curves
([Fe/H] = -1, -1.5, -2) with the
dynamical constraint (Fig. 1),
we conclude that PGCCs can be self-enriched
up to metallicities typical of the galactic halo without necessarily being
disrupted by the SNII explosions. More particularly, a PGCC whose mass
is the Bonner-Ebert mass can be self-enriched up to a level of [Fe/H]=-1.5.
Furthermore, as the position of the dynamical constraint among the
iso-metallicity curves depends on the hot protogalactic background pressure,
(see Eq.(9)), the self-enrichment level depends on the location of
the PGCC in the protogalaxy. Therefore, this model is able to explain the
metallicity gradient observed in the Old Halo (Zinn, 1992).
(See also G. Parmentier et al., Poster Section IV, this meeting)
.
Indeed, even if they release negligible amounts of heavy elements,
their dynamical impact on the PGCC must be considered.
From the comparison between these iso-metallicity curves
([Fe/H] = -1, -1.5, -2) with the
dynamical constraint (Fig. 1),
we conclude that PGCCs can be self-enriched
up to metallicities typical of the galactic halo without necessarily being
disrupted by the SNII explosions. More particularly, a PGCC whose mass
is the Bonner-Ebert mass can be self-enriched up to a level of [Fe/H]=-1.5.
Furthermore, as the position of the dynamical constraint among the
iso-metallicity curves depends on the hot protogalactic background pressure,
(see Eq.(9)), the self-enrichment level depends on the location of
the PGCC in the protogalaxy. Therefore, this model is able to explain the
metallicity gradient observed in the Old Halo (Zinn, 1992).
(See also G. Parmentier et al., Poster Section IV, this meeting)
References

|
Castor J., McCray R., Weaver R., 1975, ApJ 200, L107
Cayrel R., 1986, A&A 168, 81
Brown J.H., Burkert A., Truran J.W., 1991, ApJ 376, 115
Brown J.H., Burkert A., Truran J.W., 1995, ApJ 440, 666
Fall S.M., Rees M.J., 1985, ApJ 298, 18
Parmentier G., Jehin E., Magain P.Neuforge C., Noels A., Thoul A.A.,
1999, accepted for publication in A&A
Zinn, R., 1992, Graeme H. Smith, Jean P.Brodie, eds, ASP Conference
Series, Volume 48, The globular clusters-galaxy connection, p 38
Retour
Back
Institut d'Astrophysique et de
Géophysique de l'
Université de Liège
Avenue de Cointe, 5
B-4000 Liège, BELGIQUE
Tel: +32 (0)4 252.99.80
Fax: +32 (0)4 252.74.74
Web pages:
Sandrine Sohy
Last modification: October,31 2000.






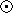 and R100, its radius in units of 100 parsecs.
and R100, its radius in units of 100 parsecs.





 ).
Using the hypothesis about PGCCs
and appropriate units, we get Eq. (7) giving the velocity of the
shell (in units of 10km.s-1) for a given PGCC mass, a given hot
protogalactic pressure and given number
of SNeII.
).
Using the hypothesis about PGCCs
and appropriate units, we get Eq. (7) giving the velocity of the
shell (in units of 10km.s-1) for a given PGCC mass, a given hot
protogalactic pressure and given number
of SNeII. 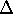 t6 is the SN
phase duration expressed in millions years.
t6 is the SN
phase duration expressed in millions years.



 under the assumed conditions;
c is the sound speed in the cloud material) can sustain more then
300 SNeII.
under the assumed conditions;
c is the sound speed in the cloud material) can sustain more then
300 SNeII.

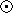 are assumed to
release a mass mz=0.3m-3.5
(in units of M
are assumed to
release a mass mz=0.3m-3.5
(in units of M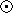 )
of heavy elements. The total number of supernovae also take into
account those whose mass is between 9 and
12 M
)
of heavy elements. The total number of supernovae also take into
account those whose mass is between 9 and
12 M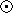 .
Indeed, even if they release negligible amounts of heavy elements,
their dynamical impact on the PGCC must be considered.
From the comparison between these iso-metallicity curves
([Fe/H] = -1, -1.5, -2) with the
dynamical constraint (Fig. 1),
we conclude that PGCCs can be self-enriched
up to metallicities typical of the galactic halo without necessarily being
disrupted by the SNII explosions. More particularly, a PGCC whose mass
is the Bonner-Ebert mass can be self-enriched up to a level of [Fe/H]=-1.5.
Furthermore, as the position of the dynamical constraint among the
iso-metallicity curves depends on the hot protogalactic background pressure,
(see Eq.(9)), the self-enrichment level depends on the location of
the PGCC in the protogalaxy. Therefore, this model is able to explain the
metallicity gradient observed in the Old Halo (Zinn, 1992).
(See also G. Parmentier et al., Poster Section IV, this meeting)
.
Indeed, even if they release negligible amounts of heavy elements,
their dynamical impact on the PGCC must be considered.
From the comparison between these iso-metallicity curves
([Fe/H] = -1, -1.5, -2) with the
dynamical constraint (Fig. 1),
we conclude that PGCCs can be self-enriched
up to metallicities typical of the galactic halo without necessarily being
disrupted by the SNII explosions. More particularly, a PGCC whose mass
is the Bonner-Ebert mass can be self-enriched up to a level of [Fe/H]=-1.5.
Furthermore, as the position of the dynamical constraint among the
iso-metallicity curves depends on the hot protogalactic background pressure,
(see Eq.(9)), the self-enrichment level depends on the location of
the PGCC in the protogalaxy. Therefore, this model is able to explain the
metallicity gradient observed in the Old Halo (Zinn, 1992).
(See also G. Parmentier et al., Poster Section IV, this meeting)



