We revisit the most often encountered argument against
self-enrichment in globular clusters, namely the ability of a
few number of supernovae to disrupt the proto-globular cloud.
We show that, within the context of the Fall and Rees theory,
primordial proto-globular cluster clouds may sustain several
hundreds of Type II supernovae. Furthermore, the corresponding
self-enrichment level is in agreement with galactic halo globular cluster
metallicities.
1. The EASE Scenario

|
Accurate abundance determinations among a sample of 21 mildly
metal-poor stars ([Fe/H] 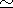 -1)
have revealed the existence of two sub-populations
of halo and thick disk field stars, namely Population IIa (hereafter PopIIa)
and Population IIb (hereafter PopIIb).
They differ by the behaviour of the s-process element
versus the
-1)
have revealed the existence of two sub-populations
of halo and thick disk field stars, namely Population IIa (hereafter PopIIa)
and Population IIb (hereafter PopIIb).
They differ by the behaviour of the s-process element
versus the  element abundances.
The PopIIa shows a correlation
between the relative abundances of light s-process elements, e.g. Y,
and
element abundances.
The PopIIa shows a correlation
between the relative abundances of light s-process elements, e.g. Y,
and  elements, e.g. Ti, with a slope smaller
than one. The PopIIb
presents a constant and maximum [Ti/Fe] value and varying values of [Y/Fe]
starting at the maximum value reached by the PopIIa.
Stars more metal-poor than [Fe/H] = -1 also follow these
correlations, while the disk stars do not.
Therefore, low metallicity stars do follow
a universal relation described by the {\it two-branches diagram},
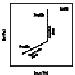
schematically illustrated in Fig. 1.
elements, e.g. Ti, with a slope smaller
than one. The PopIIb
presents a constant and maximum [Ti/Fe] value and varying values of [Y/Fe]
starting at the maximum value reached by the PopIIa.
Stars more metal-poor than [Fe/H] = -1 also follow these
correlations, while the disk stars do not.
Therefore, low metallicity stars do follow
a universal relation described by the {\it two-branches diagram},
schematically illustrated in Fig. 1.
In [1], we have suggested a scenario which
closely relates the origin of these stars to early globular cluster
(hereafter GC) evolution. Indeed, GCs might provide halo
and thick disk field stars through various dynamical processes, such as
dislocation or evaporation.
According to this scenario, PopIIa and PopIIb are related to two
different stages of the GC's chemical evolution.
In the first phase, some Type II supernovae (hereafter SNeII),
from a first generation of metal-free stars, enrich the medium
in heavy elements, notably in  elements.
This is the self-enrichment process. In the second phase,
low-mass stars accrete material ejected by AGB stars,
enriching their surface in s-process elements.
Depending on the time at which stars are ejected from GCs,
during the first phase or after the onset of the second one,
they will define either PopIIa or PopIIb. This is the scenario EASE,
Evaporation/Accretion/Self-Enrichment.
Both EASE chemical stages, namely self-enrichment and accretion,
are also illustrated
in Fig. 1.
The major goal of this work is to perform
a dynamical study of the first phase, the SNII phase.
elements.
This is the self-enrichment process. In the second phase,
low-mass stars accrete material ejected by AGB stars,
enriching their surface in s-process elements.
Depending on the time at which stars are ejected from GCs,
during the first phase or after the onset of the second one,
they will define either PopIIa or PopIIb. This is the scenario EASE,
Evaporation/Accretion/Self-Enrichment.
Both EASE chemical stages, namely self-enrichment and accretion,
are also illustrated
in Fig. 1.
The major goal of this work is to perform
a dynamical study of the first phase, the SNII phase.
2. GC Formation Through Supershell
Phenomenon

|
According to [2], the protogalaxy is a primordial two-phase medium,
made up of cold and &dense clouds embedded in a hot and diffused
protogalactic background. A typical value for the temperature of the
cold phase is 104 K, where the radiative cooling rate drops
sharply in a metal-free medium. The cold clouds are supposed
to be proto-globular cluster clouds (hereafter PGCCs), the progenitors
of galactic GCs. We will describe them as isothermal
spheres in hydrostatic equilibrium - their density profile
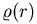 scales therefore as r-2 - and assume that there is
pressure equilibrium at the interface between the hot and the cold media.
According to the Schmidt law, the denser the medium is, the quicker the
stars will form. We therefore expect the formation of a first generation
of stars in the PGCC central regions. After a few millions years,
the massive stars of this first generation explode as SNeII.
The blast waves associated with the explosions trigger the formation and
the expansion of a supershell in which all the cloud material is swept.
This supershell gets chemically enriched with the heavy elements
released by the SNeII.
Since the cloud has produced its own source
of chemical enrichment, this phenomenon is called self-enrichment.
In the supershell, in which all the cloud material gets compressed,
the formation of a second generation of stars is triggered.
This second generation forms a proto-globular cluster.
In what follows, we restrict our analysis to halo GCs.
scales therefore as r-2 - and assume that there is
pressure equilibrium at the interface between the hot and the cold media.
According to the Schmidt law, the denser the medium is, the quicker the
stars will form. We therefore expect the formation of a first generation
of stars in the PGCC central regions. After a few millions years,
the massive stars of this first generation explode as SNeII.
The blast waves associated with the explosions trigger the formation and
the expansion of a supershell in which all the cloud material is swept.
This supershell gets chemically enriched with the heavy elements
released by the SNeII.
Since the cloud has produced its own source
of chemical enrichment, this phenomenon is called self-enrichment.
In the supershell, in which all the cloud material gets compressed,
the formation of a second generation of stars is triggered.
This second generation forms a proto-globular cluster.
In what follows, we restrict our analysis to halo GCs.
This scenario was proposed by [3] and further developed by [4] and [5].
However, even after these works, a recurrent argument
has often been used against self-enrichment, namely the SN energetics.
Since the binding energy of GCs today is
of the same order of magnitude than the kinetic
energy released by one SNII, several authors, e.g. [6],
have concluded that a still gaseous proto-cluster could be immediately
disrupted. Therefore, GCs could not be self-enriched.
However, it is important to distinguish the kinetic
energy released by the exploding stars from the kinetic
energy effectively deposited in the Interstellar Medium (hereafter ISM).
We therefore suggest another
criterion for disruption: the equality between the binding energy of
the cloud and the kinetic energy of the shell when all the cloud has
just been swept ([7]).
6. Self-Enrichment Level

|
Is the dynamical limit defined above
in agreement with the metallicities observed in galactic halo GCs ?
To answer this question, we define relations between
the mass of a primordial gas cloud
and the number of SNeII necessary to reach a given final metallicity.
We assume that each massive star whose mass m is at least
12 M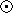 releases a mass of metals given by 0.3m - 3.5
(in units of one solar mass) [9].
The upper limit of the spectrum is assumed to be
60 M
releases a mass of metals given by 0.3m - 3.5
(in units of one solar mass) [9].
The upper limit of the spectrum is assumed to be
60 M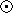 .
The stars whose mass is between 9 and
12 M
.
The stars whose mass is between 9 and
12 M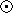 release unsignificant amounts of heavy elements.
However, their dynamical impact on the cloud must be considered and
they are therefore included in the total number N of SNeII.
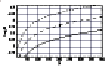
In Fig. 2, the relations between
Log M and N for three
given metallicities, typical of the galactic halo
([Fe/H]= -1, -1.5 and -2) are shown,
as well as the dynamical constraint defined in Sect. 5
for a protogalactic background pressure of
2.5 × 10-10 dyne.cm-2.
We see that a metallicity of -1.5 can be reached through self-enrichment.
Therefore, the self-enrichment
process may provide a clue to the metal amounts observed today in
galactic halo GCs.
release unsignificant amounts of heavy elements.
However, their dynamical impact on the cloud must be considered and
they are therefore included in the total number N of SNeII.
In Fig. 2, the relations between
Log M and N for three
given metallicities, typical of the galactic halo
([Fe/H]= -1, -1.5 and -2) are shown,
as well as the dynamical constraint defined in Sect. 5
for a protogalactic background pressure of
2.5 × 10-10 dyne.cm-2.
We see that a metallicity of -1.5 can be reached through self-enrichment.
Therefore, the self-enrichment
process may provide a clue to the metal amounts observed today in
galactic halo GCs.
An interesting consequence of this model is the dependence
on the value of Ph
of the location of the dynamical constraint among the iso-metallicity curves
(see (2) and (8)).
The higher the pressure is, the higher the
final metallicity will be.
Therefore, this model provides an explanation to the metallicity gradient
observed throughout the Old Halo [10].


 -1)
have revealed the existence of two sub-populations
of halo and thick disk field stars, namely Population IIa (hereafter PopIIa)
and Population IIb (hereafter PopIIb).
They differ by the behaviour of the s-process element
versus the
-1)
have revealed the existence of two sub-populations
of halo and thick disk field stars, namely Population IIa (hereafter PopIIa)
and Population IIb (hereafter PopIIb).
They differ by the behaviour of the s-process element
versus the  element abundances.
The PopIIa shows a correlation
between the relative abundances of light s-process elements, e.g. Y,
and
element abundances.
The PopIIa shows a correlation
between the relative abundances of light s-process elements, e.g. Y,
and  elements, e.g. Ti, with a slope smaller
than one. The PopIIb
presents a constant and maximum [Ti/Fe] value and varying values of [Y/Fe]
starting at the maximum value reached by the PopIIa.
Stars more metal-poor than [Fe/H] = -1 also follow these
correlations, while the disk stars do not.
Therefore, low metallicity stars do follow
a universal relation described by the {\it two-branches diagram},
schematically illustrated in Fig. 1.
elements, e.g. Ti, with a slope smaller
than one. The PopIIb
presents a constant and maximum [Ti/Fe] value and varying values of [Y/Fe]
starting at the maximum value reached by the PopIIa.
Stars more metal-poor than [Fe/H] = -1 also follow these
correlations, while the disk stars do not.
Therefore, low metallicity stars do follow
a universal relation described by the {\it two-branches diagram},
schematically illustrated in Fig. 1.  elements.
This is the self-enrichment process. In the second phase,
low-mass stars accrete material ejected by AGB stars,
enriching their surface in s-process elements.
Depending on the time at which stars are ejected from GCs,
during the first phase or after the onset of the second one,
they will define either PopIIa or PopIIb. This is the scenario EASE,
Evaporation/Accretion/Self-Enrichment.
Both EASE chemical stages, namely self-enrichment and accretion,
are also illustrated
in Fig. 1.
The major goal of this work is to perform
a dynamical study of the first phase, the SNII phase.
elements.
This is the self-enrichment process. In the second phase,
low-mass stars accrete material ejected by AGB stars,
enriching their surface in s-process elements.
Depending on the time at which stars are ejected from GCs,
during the first phase or after the onset of the second one,
they will define either PopIIa or PopIIb. This is the scenario EASE,
Evaporation/Accretion/Self-Enrichment.
Both EASE chemical stages, namely self-enrichment and accretion,
are also illustrated
in Fig. 1.
The major goal of this work is to perform
a dynamical study of the first phase, the SNII phase.

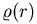 scales therefore as r-2 - and assume that there is
pressure equilibrium at the interface between the hot and the cold media.
According to the Schmidt law, the denser the medium is, the quicker the
stars will form. We therefore expect the formation of a first generation
of stars in the PGCC central regions. After a few millions years,
the massive stars of this first generation explode as SNeII.
The blast waves associated with the explosions trigger the formation and
the expansion of a supershell in which all the cloud material is swept.
This supershell gets chemically enriched with the heavy elements
released by the SNeII.
Since the cloud has produced its own source
of chemical enrichment, this phenomenon is called self-enrichment.
In the supershell, in which all the cloud material gets compressed,
the formation of a second generation of stars is triggered.
This second generation forms a proto-globular cluster.
In what follows, we restrict our analysis to halo GCs.
scales therefore as r-2 - and assume that there is
pressure equilibrium at the interface between the hot and the cold media.
According to the Schmidt law, the denser the medium is, the quicker the
stars will form. We therefore expect the formation of a first generation
of stars in the PGCC central regions. After a few millions years,
the massive stars of this first generation explode as SNeII.
The blast waves associated with the explosions trigger the formation and
the expansion of a supershell in which all the cloud material is swept.
This supershell gets chemically enriched with the heavy elements
released by the SNeII.
Since the cloud has produced its own source
of chemical enrichment, this phenomenon is called self-enrichment.
In the supershell, in which all the cloud material gets compressed,
the formation of a second generation of stars is triggered.
This second generation forms a proto-globular cluster.
In what follows, we restrict our analysis to halo GCs. 
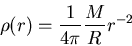
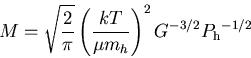
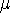 ,
its mean molecular weight (
,
its mean molecular weight (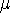 = 1.2),
G, the gravitational constant and Ph,
the pressure value of the hot
protogalactic background confining the PGCC.
= 1.2),
G, the gravitational constant and Ph,
the pressure value of the hot
protogalactic background confining the PGCC. 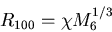
 and R100, its radius expressed in units of 100 pc.
The parameter
and R100, its radius expressed in units of 100 pc.
The parameter  is related to Ph
(expressed in dyne.cm-2) by
is related to Ph
(expressed in dyne.cm-2) by 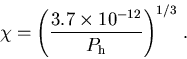

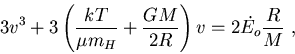
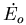 is the rate at which the SNII energy
is supplied. The second and third terms on the left-hand-side account
for the decelerating effects respectively provided by the pressure
external to the shell and by the shell gravity.
With the different hypothesis about PGCCs, (5) can be reduced to
is the rate at which the SNII energy
is supplied. The second and third terms on the left-hand-side account
for the decelerating effects respectively provided by the pressure
external to the shell and by the shell gravity.
With the different hypothesis about PGCCs, (5) can be reduced to 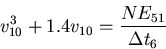
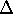 t6, the
duration of the SNII phase.
t6, the
duration of the SNII phase.

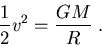
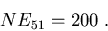

 releases a mass of metals given by 0.3m - 3.5
(in units of one solar mass) [9].
The upper limit of the spectrum is assumed to be
60 M
releases a mass of metals given by 0.3m - 3.5
(in units of one solar mass) [9].
The upper limit of the spectrum is assumed to be
60 M .
The stars whose mass is between 9 and
12 M
.
The stars whose mass is between 9 and
12 M release unsignificant amounts of heavy elements.
However, their dynamical impact on the cloud must be considered and
they are therefore included in the total number N of SNeII.
In Fig. 2, the relations between
Log M and N for three
given metallicities, typical of the galactic halo
([Fe/H]= -1, -1.5 and -2) are shown,
as well as the dynamical constraint defined in Sect. 5
for a protogalactic background pressure of
2.5 × 10-10 dyne.cm-2.
We see that a metallicity of -1.5 can be reached through self-enrichment.
Therefore, the self-enrichment
process may provide a clue to the metal amounts observed today in
galactic halo GCs.
release unsignificant amounts of heavy elements.
However, their dynamical impact on the cloud must be considered and
they are therefore included in the total number N of SNeII.
In Fig. 2, the relations between
Log M and N for three
given metallicities, typical of the galactic halo
([Fe/H]= -1, -1.5 and -2) are shown,
as well as the dynamical constraint defined in Sect. 5
for a protogalactic background pressure of
2.5 × 10-10 dyne.cm-2.
We see that a metallicity of -1.5 can be reached through self-enrichment.
Therefore, the self-enrichment
process may provide a clue to the metal amounts observed today in
galactic halo GCs.