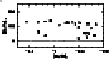Accurate relative abundances have been obtained for a sample of 21 mildly metal-poor
stars from the analysis of high resolution and high signal-to-noise spectra. In order
to reach the highest coherence and internal precision, lines with similar dependency
on the stellar atmospheric parameters were selected, and the analysis was carried out
in a strictly differential way within the sample.
With these accurate results, correlations between relative abundances have been
searched for, with a special emphasis on the neutron capture elements.
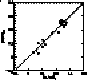
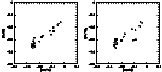
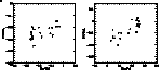
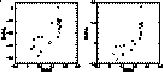
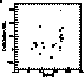
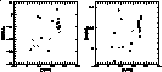
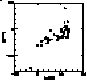
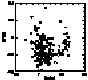
This analysis shows that the r elements are closely correlated to the
 elements, which is in agreement with the
generally accepted idea that the r-process
takes place during the explosion of massive stars.
elements, which is in agreement with the
generally accepted idea that the r-process
takes place during the explosion of massive stars.
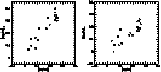
The situation is more complex as far as the s elements are concerned. Their relation
with the  elements is not linear.
In a first group of stars, the relative abundance of the s
elements increases only slightly with the
elements is not linear.
In a first group of stars, the relative abundance of the s
elements increases only slightly with the  elements
overabundance until the latter reaches a maximum value. For the second group, the
s elements show a rather large range of enhancement and a constant (and maximum)
value of the
elements
overabundance until the latter reaches a maximum value. For the second group, the
s elements show a rather large range of enhancement and a constant (and maximum)
value of the  elements overabundance.
elements overabundance.
This peculiar behaviour leads us to distinguish between two sub-populations of
metal-poor stars, namely Pop IIa (first group) and Pop IIb (second group).
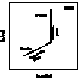
We suggest a scenario of formation of metal-poor stars based on two distinct phases
of chemical enrichment, a first phase essentially consisting in supernova explosions
of massive stars, and a second phase where the enrichment is provided by stellar
winds from intermediate mass stars.
More specifically, we assume that all thick disk and field halo stars were born
in globular clusters, from which they escaped, either during an early disruption of
the cluster (Pop IIa) or, later, through an evaporation process (Pop IIb).
References

|
Alonso, A., Arribas, S., Martinez-Roger, C. 1994, A&ASS, 107, 365
Anders, E., Grevesse, N. 1989, Geochimica et Cosmochimica Acta, 53, 197
Andersen, T., Poulsen, O., Ramanujam, P.S., Petrakiev-Petkov, A. 1975, Sol. Phys., 44, 257
Armandroff, T.E. 1989, AJ, 97, 375
Arnesen, A., Bengtsson, A., Halling, R., Lindskog, J., Nordling, C., Noreland, T. 1977a,
Phys. Scr. 16, 31
Arnesen, A., Bengtsson, A., Halling, R., Noreland, T. 1977b, J. Phys. B, 10, 565
Arnett, D. 1991, in Frontiers of Stellar Evolution, ASP Conf.
Ser. 20, 389
Barbier-Brossat, M., Petit, M., Figon, P. 1994, A&ASS 108, 603
Becker, O., Enders, K., Werth, G., Dembczynski, J. 1993, Phys. Rev. A, 48, 3546
Biémont, E., Grevesse, N., Lowe, R.M., Hannaford, P. 1981, ApJ 248, 867
Biémont, E., Kerner, C., Meyer, G., Träger F., zu Putlitz G. 1982, A&A 107,
166
Biémont, E., Grevesse, N., Hannaford, P., Lowe, R.M. 1989, A&A 222, 307
Blackwell, D.E., Shallis, M.J. 1977, MNRAS 180, 177
Blackwell, D.E., Menon, S.L.R., Petford, A.D. 1984, MNRAS 207, 533
Blackwell, D.E., Petford, A.D., Simmons, G.J. 1982a, MNRAS 201, 595
Blackwell, D.E., Booth, A.J., Menon, S.L.R., Petford, A.D. 1986a, MNRAS 220, 289
Blackwell, D.E., Booth, A.J., Menon, S.L.R., Petford, A.D. 1986b, MNRAS 220, 303
Blackwell, D.E., Booth, A.J., Petford, A.D., Shallis, M.J., Leggett, S. 1982b, MNRAS 199,
21
Broström, L., Mannervik, S., Royen,, P., Wännström A. 1995, Phys. Scr. 51, 330
Brown, J.H., Burkert, A., Truran, J.W. 1995, ApJ, 440, 666
Carney, B.W. 1983, AJ 88, 623
Carney, B.W. 1996, PASP 108, 900
Cayrel, R. 1986, A&A 168, 81
Corliss, C.H., Bozman, W.R. 1962, Experimental Transition Probabilities for Spectral lines of
Seventy Elements (NBS Monograph 32) (Washington: GPO)
Doerr, A., Kock, M. 1985, J. Quant. Spectrosc. Radiat. Transfer, 33, 307
ESA, 1997, 'The HIPPARCOS Catalogue', ESA SP-1200, ESTEC, Nordwijk
Edvardsson, B., Andersen, J., Gustafsson, B., Lambert, D.L., Nissen, P.E., Tomkin, J. 1993,
A&A, 275, 101
Evans, D.S. 1967, Catalogue of Stellar Radial Velocities, IAU Symp. 30, 57
Gallagher, A. 1967, Phys. Rev. 157, 24
Gosset, E., Magain, P. 1993, ESO Messenger 73, 13
Gratton, R.G., Sneden, C. 1991, A&A 241, 501
Gratton, R.G., Sneden, C. 1994, A&A 287, 927
Gray, D.F. 1972 The Observation and Analysis of Stellar Photospheres,
Wiley, New York
Grevesse, N., Noels, A., Sauval, A.J. 1996, {\em Cosmic Abundances}, ASP
Conf. Series, Vol. 99, 117
Gustafsson, B., Bell, R.A., Eriksson, K., Nordlund, A. 1975, A&A 42, 407
Hannaford, P., Lowe, R.M., Grevesse, N., Biémont, E., Whaling, W. 1982, ApJ 261, 736
Harris, W.O. 1998, preprint astro-ph/9801201
Jehin, E., Magain, P., Neuforge, C., Noels, A., Thoul, A.A. 1998, A&A 330, L33
Johnson, D.R.H., Soderblom, D.R. 1987, AJ, 93, 864
Kurucz, R.L. 1993, ATLAS9 Stellar Atmosphere Programs and 2 km/s grids, Kurucz CD-ROM
No 13
Magain, P. 1987, A&A 181, 323
Meylan, G., Heggie, D.C. 1997, Astron. Astrophys. Rev., 8, 1
Migdalek, J., Baylis, W.E. 1987, Can. J. Phys. 65, 1612
Mihalas, D., Routly, P.M. 1968, Galactic Astronomy, Freeman and Co.
Möller, W., Hürnermann, H., Alkhazov, G., Panteleev, V. 1993, Phys. Rev. Lett. 70,
541
Morgan, S., Lake, G. 1989, ApJ, 339, 171
Nissen, P.E., Schuster, W.J. 1997, A&A, 326, 751
Nissen, P.E., Høg, E., Schuster, W.J. 1998, Proc. of Hipparcos Venice 97 Symposium,
ESA SP-402, in press
Olsen, E.H., 1994, A&AS 106, 257
Schuster, W.J., Nissen, P.E. 1988, A&ASS 73, 225
Smith, G. 1986, PASP, 99, 67
Smith, G. 1987, ApJ, 306, 565
Smith ,G., Raggett, D. St J. 1981, J.Phys. B: At. Mol. Phys. 14, 4015
Thielemann, F.K., Nomoto, K., Hashimoto, M. 1993, in Origin and
Evolution of the Elements, eds. N. Prantzos et al., Cambridge Univ. Press,
p.297
VandenBerg, D.A., Bell, R.A. 1985, ApJSS 58, 561
Villemoes, P., Wang, M. 1994, Z. Phys. D, 30, 19
Whaling, W., Hannaford, P., Lowe, R.M., Biémont, E., Grevesse, N. 1985, A&A 153, 109
Wickliffe, M.E., Lawler, J.E. 1997, ApJSS 110, 163
Wilson, R.E. 1953, General Catalog of Stellar Radial Velocities, Carnegie Inst. of
Washington, Washington, D.C.
Wiese, W.L., Martin, G.A. 1980, NSRDS-NBS 68 (U.S. Gov. Printing Office, Washington, DC)
Woolf, V.M., Tomkin, J., Lambert, D.L. 1995, ApJ 453, 660
Woosley, S.E., Weaver, T.A. 1995, ApJSS 101, 181
Zhao, G., Magain, P. 1991, A&A 244,425
Zinn, R. 1985, ApJ, 293, 424
Retour
Back
Institut d'Astrophysiqueet de
Géophysique de l'
Université de Liège
Avenue de Cointe, 5
B-4000 Liège, BELGIQUE
Tel: +32 (0)4 252.99.80
Fax: +32 (0)4 252.74.74
Web pages:
Sandrine Sohy
Last modification: september,2 1999.
 elements, which is in agreement with the
generally accepted idea that the r-process
takes place during the explosion of massive stars.
elements, which is in agreement with the
generally accepted idea that the r-process
takes place during the explosion of massive stars.  elements is not linear.
In a first group of stars, the relative abundance of the s
elements increases only slightly with the
elements is not linear.
In a first group of stars, the relative abundance of the s
elements increases only slightly with the  elements
overabundance until the latter reaches a maximum value. For the second group, the
s elements show a rather large range of enhancement and a constant (and maximum)
value of the
elements
overabundance until the latter reaches a maximum value. For the second group, the
s elements show a rather large range of enhancement and a constant (and maximum)
value of the  elements overabundance.
elements overabundance. 
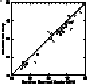
 log10(NA/NB)* - log10(NA/NB)
log10(NA/NB)* - log10(NA/NB)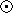 for elements A and B.
for elements A and B.
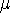 m each.
m each. 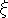 are obtained, as usual, by forcing a
set of lines of the same element and same ionization stage but with different EWs to indicate
the same abundance. In our observations, only the Fe I lines are suitable for such a
determination. The precision of the microturbulence determinations, estimated by linear
regression, is better than 0.1 km s-1.
The adopted model parameters for the 21 stars are listed in
are obtained, as usual, by forcing a
set of lines of the same element and same ionization stage but with different EWs to indicate
the same abundance. In our observations, only the Fe I lines are suitable for such a
determination. The precision of the microturbulence determinations, estimated by linear
regression, is better than 0.1 km s-1.
The adopted model parameters for the 21 stars are listed in
 )
relations) of Kurucz (1993).
Given the T(
)
relations) of Kurucz (1993).
Given the T(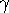 were computed
with the Uns\"old formula (Gray 1972), with an empirical enhancement factor of 1.5.
were computed
with the Uns\"old formula (Gray 1972), with an empirical enhancement factor of 1.5.  > ~ 0.03).
In the case of Fe and Cr,
both neutral and ionized lines are available.
> ~ 0.03).
In the case of Fe and Cr,
both neutral and ionized lines are available.  [Fe/H]
[Fe/H]