|Home|Atmospheric Lensing|Gravitational Lensing|GL Experiment|Examples|References|
For didactical purposes, it is very useful to construct and use optical lenses
that mimic the deflection of light rays as derived in Eq. (2.1) for the case of axially symmetric gravitational lenses. Such optical lenses should of
course be rotationally symmetric, flat on one side (for simplicity) and have,
on the other side, a surface determined in such a way that rays characterized
by an impact parameter ![]() gets deflected by the angle
gets deflected by the angle ![]() (see Eq. (2.1) and Fig. 1). Optical lenses simulating the light deflection properties due to a point mass (cf. a black hole), a singular isothermal sphere and a spiral galaxy have been manufactured by the authors (see Figs. 2 and 3). A detailed description of their shapes is proposed in exercise 3.
(see Eq. (2.1) and Fig. 1). Optical lenses simulating the light deflection properties due to a point mass (cf. a black hole), a singular isothermal sphere and a spiral galaxy have been manufactured by the authors (see Figs. 2 and 3). A detailed description of their shapes is proposed in exercise 3.
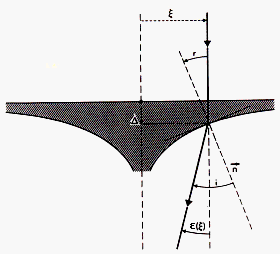 Figure 1: Deflection of a light ray passing through an axially symmetric optical lens
Figure 1: Deflection of a light ray passing through an axially symmetric optical lens
3.1. Exercise 3: Shapes of axially symmetric optical lenses
Applying Descartes's law (cf. Eq. (1.2)) to the ray depicted in Fig. 1 and
assuming that the angles (r and i) between the normal ![]() to the optical surface and the incident and refracted rays are very small, we may write the
relation
to the optical surface and the incident and refracted rays are very small, we may write the
relation
![]()
where n represents here the refractive index of the lens with respect to the air. Furthermore, since we have
![]()
and that the tangent to the optical surface at the point (![]() ) is merely given by (see Fig. 1)
) is merely given by (see Fig. 1)
![]()
it is straigtforward to derive the shape of a lens by means of the following differential equation
![]()
3.1.1. The optical point mass lens
By definition, the mass M of a point lens model is concentrated in one point such that we have ![]() . It is then simple to solve Eq. (3.4) and derive the thickness
. It is then simple to solve Eq. (3.4) and derive the thickness ![]() of the corresponding optical lens as a function of the impact parameter
of the corresponding optical lens as a function of the impact parameter ![]() . We find that
. We find that
![]()
where ![]() represents the Schwarzschild radius of the compact lens. In practice, the point
represents the Schwarzschild radius of the compact lens. In practice, the point ![]() is chosen in order to specify a given thickness (e.g.
is chosen in order to specify a given thickness (e.g. ![]() ) for the optical lens at a selected radius (e.g.
) for the optical lens at a selected radius (e.g. ![]() ). The resulting shape of such an optical 'point mass' lens is illustrated in Fig. 2a. It looks very much like the foot of some glasses of wine which, therefore, have been commonly used in the past by some astronomers to simulate lensing effects. A realistic 'point mass' lens, made of plexiglas-like material (refractive index n = 1.49 and a diameter of 30cm has been manufactured by the authors for the particular value of Rsc=0.3cm, corresponding to the Schwarzschild radius of one third of the Earth mass (see Fig. 3, left).
). The resulting shape of such an optical 'point mass' lens is illustrated in Fig. 2a. It looks very much like the foot of some glasses of wine which, therefore, have been commonly used in the past by some astronomers to simulate lensing effects. A realistic 'point mass' lens, made of plexiglas-like material (refractive index n = 1.49 and a diameter of 30cm has been manufactured by the authors for the particular value of Rsc=0.3cm, corresponding to the Schwarzschild radius of one third of the Earth mass (see Fig. 3, left).

Figure 2: Several examples of axially symmetric optical lenses
simulating the light deflection properties due to a point mass (a), a SIS
galaxy (b) and a spiral galaxy (c)
 Figure 3: Examples of a 'point mass' (left)
and a 'spiral galaxy' (right) optical lens produced by the
authors. We have used these particular lenses, made of plexiglas-like
material (n = 1.49, 30 cm in diameter), to simulate the formation of
multiple images of a distant source. The optical gravitational lens experiment
is described in section 4
Figure 3: Examples of a 'point mass' (left)
and a 'spiral galaxy' (right) optical lens produced by the
authors. We have used these particular lenses, made of plexiglas-like
material (n = 1.49, 30 cm in diameter), to simulate the formation of
multiple images of a distant source. The optical gravitational lens experiment
is described in section 4
3.1.2. The SIS optical lens
For the case of a singular isothermal sphere (hereafter SIS) lens model, it
is well known that the mass of such a galaxy increases linearly with the
impact parameter ![]() , i.e.
, i.e. ![]() . We may thus rewrite
Eq. (3.4) in the form
. We may thus rewrite
Eq. (3.4) in the form
![]()
where K represents a positive constant. Integration of the above equation leads to the solution
![]()
The shape of the resulting SIS lens is thus merely an axially symmetric cone as illustrated in Fig. 8b.
3.1.3. The 'spiral galaxy' optical lens
Given the exponential surface mass density
![]()
which describes reasonably well the mass distribution of a spiral galaxy disk
having a characteristic size ![]() , we may derive the mass distribution
, we may derive the mass distribution
![]() of such a deflector by means of the relation
of such a deflector by means of the relation
![]()
Integration of this last expression leads immediately to the result
![]()
Inserting this result into Eq. (3.4) and performing the integration, we find that
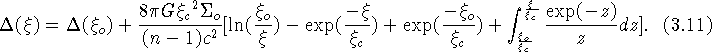
The general shape of a 'spiral galaxy' optical lens is illustrated in
Fig. 2c. A 30 cm diameter 'spiral galaxy' lens, produced by the authors, is shown in Fig. 3 (right). This lens is characterized by the following physical parameters: an equivalent Schwarzschild radius of one third of the Earth mass,
i.e. ![]() (see Eq. (3.10)),
(see Eq. (3.10)), ![]() ,
, ![]() and
and ![]() .
.
In order to simulate the formation of lensed images by a given mass distribution (point mass, etc.), we have used the optical setup that is shown in Fig. 1.

A compact light source is located on the left side (not clearly seen), then comes the point mass optical lens (cf. Fig. 3, in section 3, left) that deflects the light rays very nearly as a black hole having one third of the Earth mass. Behind the lens, we find a white screen with a small hole at the center (pinhole lens). Further behind, there is a large screen on which is projected the lensed image(s) of the source (the Einstein ring, in this case) as it would be seen if our eye were located at the position of the pinhole. In the example illustrated here, the pinhole is set very precisely on the optical axis of the gravitational lens so that the source, the lens and the pinhole (observer) are perfectly aligned. Some smoke in this experiment reveals the existence of a bright `pseudo- focal' line along the optical axis. Intersection of this line with the pinhole screen thus consists of a bright white spot (cf. Figure 2a). Note that the bright regions seen on the lens in Fig. 1 are essentially caused by scattered light. Let us now produce a second type of gravitational lens mirage: as we move the pinhole very slightly away from the symmetry axis (Fig. 2b), the Einstein ring breaks in two images which angular separation remains comparable with the diameter of the Einstein ring (Fig. 2c).
 |  |  |
The effects of a typical non symmetric (singular) gravitational lens may be simulated by simply tilting the optical lens around its vertical axis. In this case (see Fig. 3a), the bright (focal) line along the optical axis which existed in the symmetric configuration (cf. Fig. 2a) has changed into a two dimensional caustic surface, a section of which is seen as a diamond shaped caustic (made of four folds and four cusps) in the pinhole plane. As a result, the Einstein ring that was observed in the symmetric case has now split up into four lensed images (Fig. 3b). Such a configuration of four lensed images always arises when the pinhole (observer) lies inside the diamond formed by the caustic. Let us immediately note that such caustics constitute a generic property of gravitational lensing, the focal line in the symmetric configuration being just a degenerate case. Fig. 3d shows the merging of two of the four images into one, single, bright image when the pinhole approaches one of the fold caustics (Fig. 3c). Just after the pinhole has passed the fold caustic (see Fig. 3e), the two merging images have totally disappeared (Fig. 3f).

A particularly interesting case occurs when the pinhole (observer) is located very close to one of the cusps (cf. Fig. 3g). Three of the four previous images have then merged into one luminous arc, whereas the fourth one appears as a faint counterimage (Fig. 3h). For large sources that cover most of the diamond shaped caustic (Fig. 3i), an almost complete Einstein ring is observed (Fig. 3j), although the source, lens and observer are not perfectly aligned and the lens is still being tilted. In this last experiment, the increase of the source size has been simulated by enlarging the pinhole radius by a factor 4. In order to show that this is a correct simulation, one may consider the pinhole and the screen behind it as a camera. It is then clear that an increase in the size of the pinhole leads to a larger and less well focused image of the compact source, corresponding indeed to an increase in the source size. A more detailed and rigorous analysis does confirm this result.
In Table1, we are presenting known gravitational lens systems which display image configurations similar to the generic ones simulated in the gravitational lens experiment.
This optical gravitational lens experiment may also be used to simulate the formation of multiple giant luminous arcs and arclets seen near massive foreground galaxy clusters. In order to do so, we may simply replace the single pinhole screen by a cardboard perforated with multiple pinholes. In the absence of light deflection (i.e. by simply removing the optical lens), direct (non distorted) images of the circular background galaxies would be seen by an observer, alike those projected on the distant white screen (Fig. 4, left).

When inserting the optical lens between the light source and the multiple pinholes screen, images of the background galaxies get distorted (arclets) and/or transformed into multiple images, including giant luminous arcs (see Figs. 4 middle and right as possible examples). While covering the pinholes with various transparent colored filters, the distorted background galaxies look very much like those observed with the Hubble Space Telescope around the foreground galaxy cluster Abell 2218 (see HST press release). More generally speaking, the image configurations illustrated in Figs. 3a-j and 2b-c are all found among the observed gravitational lens systems accessible on one of our web pages (click here). It is of course obvious that if our optical lens would have been constructed non-singular in the center (cf. the 'spiral galaxy' optical lens shown in Fig. 3, section 3, right), we would have seen an additional image formed in the central part of the lens. For most of the known lenses with an even number of observed images, it may well be that a black hole resides in the center of the lens. The presence of a compact core could also account for the "missing" image since then the very faint image expected to be seen close to, or through the core, would be well below the detection limits that are presently achievable.