For didactical purposes, it is very useful to construct and use optical lenses that mimic the deflection of light rays as derived in Eq. (2.1) for the case of axially symmetric gravitational lenses. Such optical lenses should of course be rotationally symmetric, flat on one side (for simplicity) and have, on the other side, a surface determined in such a way that rays characterized by an impact parameter gets deflected by the angle (see Eq. (2.1) and Fig. 1). Optical lenses simulating the light deflection properties due to a point mass (cf. a black hole), a singular isothermal sphere and a spiral galaxy have been manufactured by the authors (see Figs. 2 and 3). A detailed description of their shapes is proposed in exercise 3.

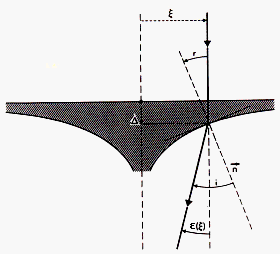Figure 1: Deflection of a light ray passing through an axially symmetric optical lens

3.1. Exercise 3: Shapes of axially symmetric optical lenses

Applying Descartes's law (cf. Eq. (1.2)) to the ray depicted in Fig. 1 and assuming that the angles (r and i) between the normal to the optical surface and the incident and refracted rays are very small, we may write the relation

where n represents here the refractive index of the lens with respect to the air. Furthermore, since we have

and that the tangent to the optical surface at the point () is merely given by (see Fig. 1)

it is sraigtforward to derive the shape of a lens by means of the following differential equation

3.1.1. The optical point mass lens

  By definition, the mass M of a point lens model is concentrated in one point such that we have . It is then simple to solve Eq. (3.4) and derive the thickness of the corresponding optical lens as a function of the impact parameter . We find that

where represents the Schwarzschild radius of the compact lens. In practice, the point is chosen in order to specify a given thickness (e.g. ) for the optical lens at a selected radius (e.g. ). The resulting shape of such an optical 'point mass' lens is illustrated in Fig. 2a. It looks very much like the foot of some glasses of wine which, therefore, have been commonly used in the past by some astronomers to simulate lensing effects. A realistic 'point mass' lens, made of plexiglas-like material (refractive index n = 1.49 and a diameter of 30cm has been manufactured by the authors for the particular value of R_sc=0.3cm, corresponding to the Schwarzschild radius of one third of the Earth mass (see Fig. 3, left).

Figure 2: Several examples of axially symmetric optical lenses simulating the light deflection properties due to a point mass (a), a SIS galaxy (b) and a spiral galaxy (c)

Figure 3: Examples of a 'point mass' (left) and a 'spiral galaxy' (right) optical lens produced by the authors. We have used these particular lenses, made of plexiglas-like material (n = 1.49, 30 cm in diameter), to simulate the formation of multiple images of a distant source. The optical gravitational lens experiment is described in section 4

3.1.2. The SIS optical lens

For the case of a singular isothermal sphere (hereafter SIS) lens model, it is well known that the mass of such a galaxy increases linearly with the impact parameter , i.e. . We may thus rewrite Eq. (3.4) in the form

where K represents a positive constant. Integration of the above equation leads to the solution

The shape of the resulting SIS lens is thus merely an axially symmetric cone as illustrated in Fig. 8b.

3.1.3. The 'spiral galaxy' optical lens

Given the exponential surface mass density

which describes reasonably well the mass distribution of a spiral galaxy disk having a characteristic size , we may derive the mass distribution of such a deflector by means of the relation

Integration of this last expression leads immediately to the result

Inserting this result into Eq. (3.4) and performing the integration, we find that

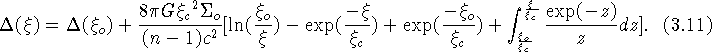
The general shape of a 'spiral galaxy' optical lens is illustrated in Fig. 2c. A 30 cm diameter 'spiral galaxy' lens, produced by the authors, is shown in Fig. 3 (right). This lens is characterized by the following physical parameters: an equivalent Schwarzschild radius of one third of the Earth mass, i.e. (see Eq. (3.10)),   ,        and   .